Use LLMs to Combine Different Responses
Universal Self Consistency1 aims to extend self-consistency by using a second LLM model to judge the quality of individual responses. Therefore instead of choosing the final answer based on the most frequently occuring value among each reasoning chain, we instead prompt the model to choose the most consistent answer for us relative to the prompt.
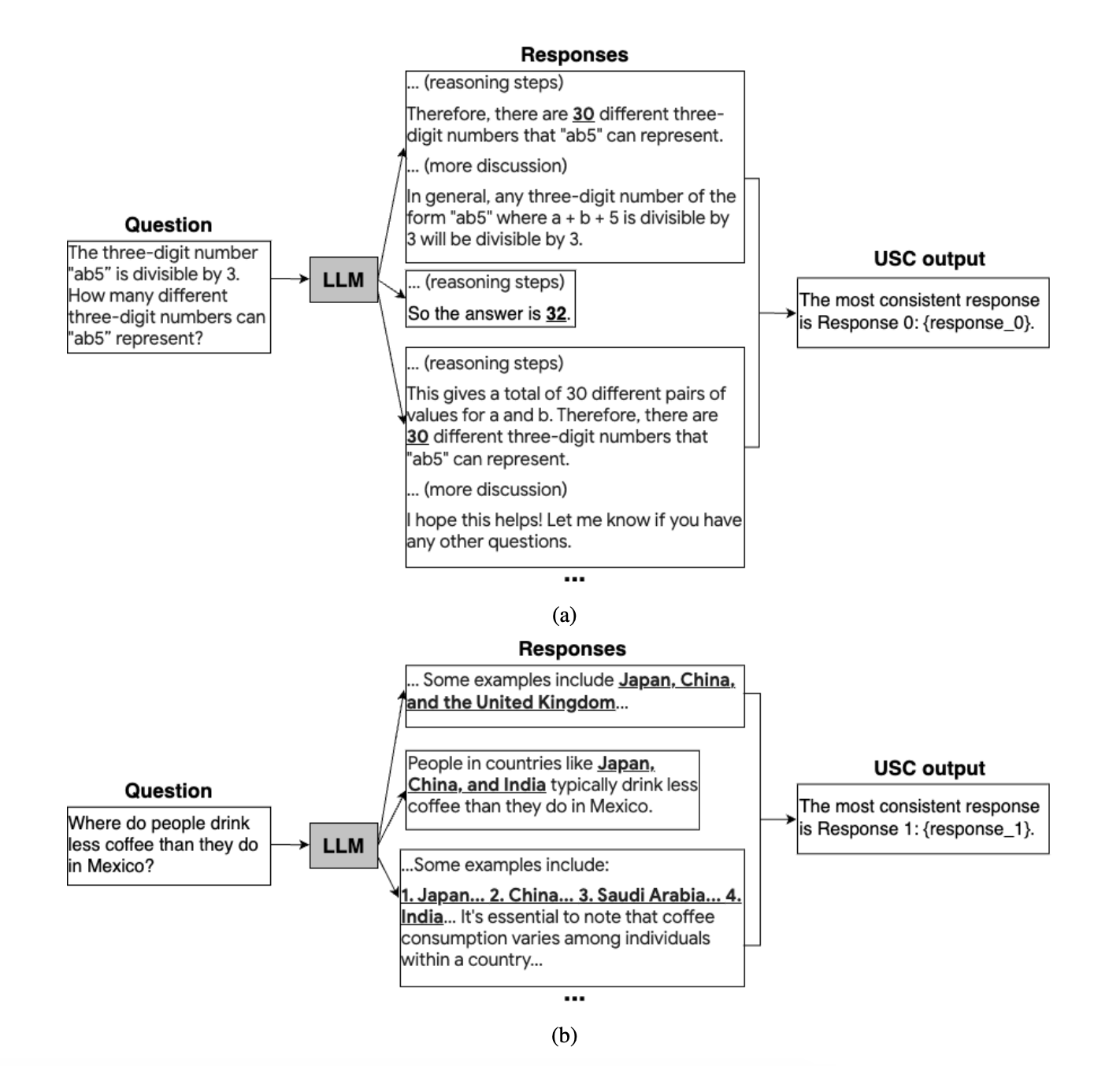
This enables us to support a greater variety of different response formats and answer, leading to greater diversity of outputs and hence higher accuracy.
We can implement this in instructor as seen below.
from pydantic import BaseModel, Field, ValidationInfo, field_validator
import instructor
from textwrap import dedent
import asyncio
client = instructor.from_provider("openai/gpt-5-nano", async_client=True)
class Response(BaseModel):
chain_of_thought: str
answer: str
class SelectedResponse(BaseModel):
most_consistent_response_id: int = Field(
description="""The ID of the most consistent response that
was provided"""
)
@field_validator("most_consistent_response_id")
@classmethod
def validate_id(cls, v: int, info: ValidationInfo):
context = info.context
number_responses = context.get("number_responses", float("inf"))
if v > number_responses:
raise ValueError(
f"""Most consistent response ID {v} is greater than the
number of responses {number_responses}. Please return a
valid id between 0 and {number_responses-1}"""
)
return v
async def generate_response(query: str) -> Response:
return await client.create(
model="gpt-4o",
response_model=Response,
messages=[{"role": "user", "content": query}],
)
async def generate_batch_responses(query: str, no_responses: int):
coros = [generate_response(query) for _ in range(no_responses)]
return await asyncio.gather(*coros)
async def select_consistent_response(responses: list[Response], query: str):
formatted_responses = "\n".join(
[
f"Response {idx}: {response.chain_of_thought}. {response.answer}"
for idx, response in enumerate(responses)
]
)
return await client.create(
model="gpt-4o",
response_model=SelectedResponse,
messages=[
{
"role": "user",
"content": dedent(
f"""
<user query>
{query}
</user query>
{formatted_responses}
Evaluate these responses.
Select the most consistent response based on majority
consensus
"""
),
}
],
context={"number_responses": len(responses)},
)
if __name__ == "__main__":
query = """The three-digit number 'ab5' is divisible by 3. How many different
three-digit numbers can 'ab5' represent?"""
responses = asyncio.run(generate_batch_responses(query, 3))
for response in responses:
print(response.model_dump_json(indent=2))
"""
{
"chain_of_thought": "A number is divisible by 3 if
the sum of its digits is divisible by 3. Given the
number 'ab5', we need to check how many different
values of 'a' and 'b', where both are digits (0-9)
can make the sum divisible by 3.\n\nThe sum of the
digits is a + b + 5.\n\nWe need to find pairs (a, b)
such that (a + b + 5) % 3 == 0.",
"answer": "30"
}
"""
"""
{
"chain_of_thought": "A number is divisible by 3 if
the sum of its digits is divisible by 3. Let's
denote the digits a and b. The number 'ab5' has
digits a, b, and 5. Therefore, the sum of the
digits is a + b + 5. Since the number is divisible
by 3, a + b + 5 must be divisible by 3.\n\nNow,
since a and b are single digits (0-9), we need to
find pairs (a, b) such that a + b + 5 is divisible
by 3. We will evaluate all possible combinations of
values for a and b to count how many valid pairs
(a, b) exist.\n\nLet's start by considering b's
values:\n1. If b = 0, then a + 5 must be divisible
by 3.\n2. If b = 1, then a + 6 must be divisible by
3.\n3. If b = 2, then a + 7 must be divisible by
3.\n4. If b = 3, then a + 8 must be divisible by
3.\n5. If b = 4, then a + 9 must be divisible by
3.\n6. If b = 5, then a + 10 must be divisible by
3.\n7. If b = 6, then a + 11 must be divisible by
3.\n8. If b = 7, then a + 12 must be divisible by
3.\n9. If b = 8, then a + 13 must be divisible by
3.\n10. If b = 9, then a + 14 must be divisible by
3.\n\nWe will find all corresponding a values for
each b and count the valid combinations.\n",
"answer": "There are 30 different three-digit
numbers that 'ab5' can represent."
}
"""
"""
{
"chain_of_thought": "A number is divisible by 3 if
the sum of its digits is divisible by 3. The given
number is in the form 'ab5', where 'a' and 'b' are
digits from 0 to 9. To find the total number of
different three-digit numbers that 'ab5' can
represent, we need to determine all possible digit
combinations for 'a' and 'b' such that 'a + b + 5'
is divisible by 3.",
"answer": "30"
}
"""
selected_response = asyncio.run(select_consistent_response(responses, query))
print(selected_response.model_dump_json(indent=2))
"""
{
"most_consistent_response_id": 0
}
"""
print(
responses[selected_response.most_consistent_response_id].model_dump_json(
indent=2
)
)
"""
{
"chain_of_thought": "A number is divisible by 3 if the sum of its digits is divisible by 3. Given the number 'ab5', we need to
check how many different values of 'a' and 'b', where both are digits (0-9) can make the sum divisible by 3.\n\nThe sum of the
digits is a + b + 5.\n\nWe need to find pairs (a, b) such that (a + b + 5) % 3 == 0.",
"answer": "30"
}
"""
References¶
1: Universal Self-Consistency For Large Language Model Generation