Skip to content

Use Ensembles To Test Prompts

What's Max Mutual Information?

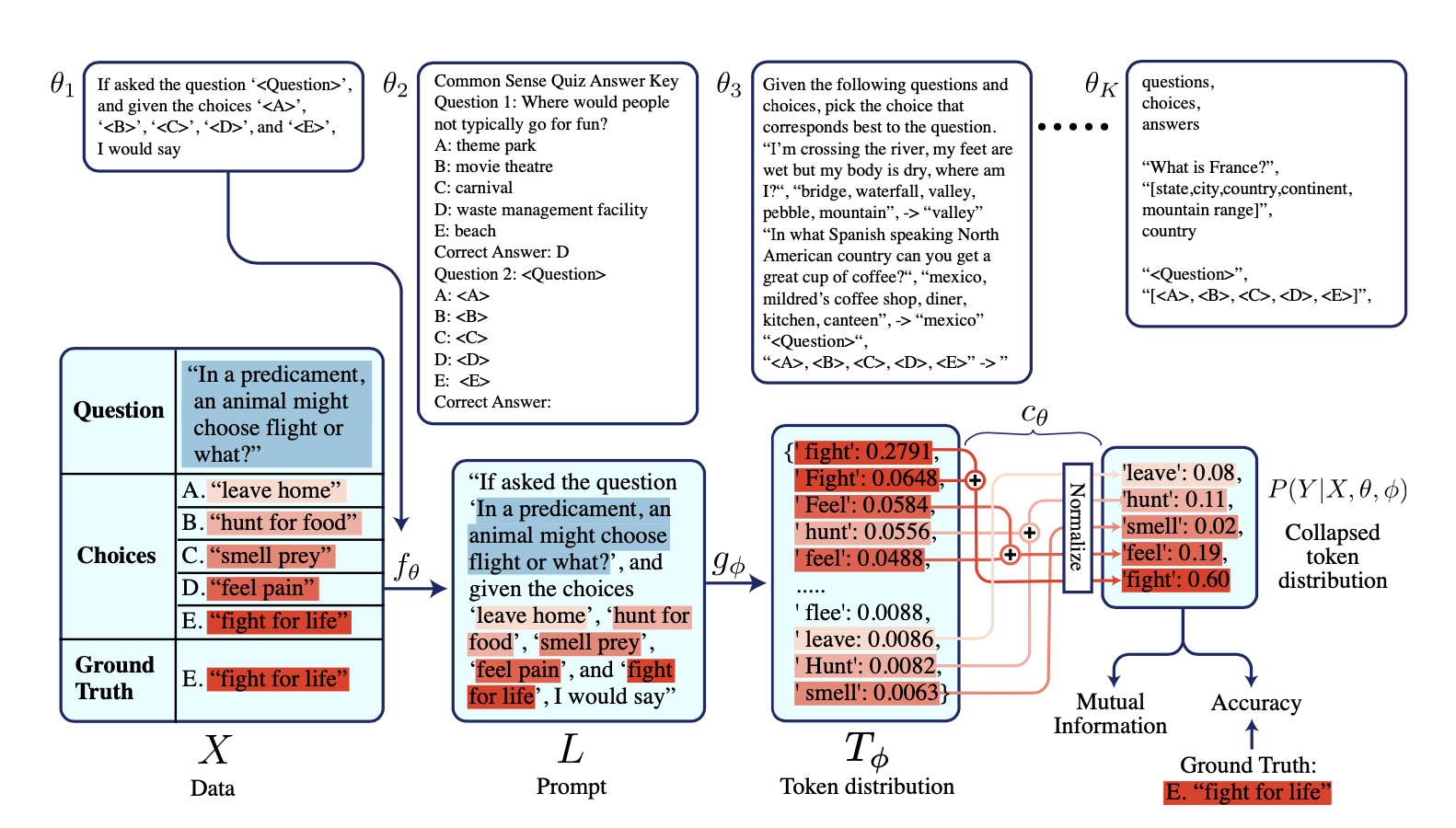
Max Mutual Information Method is a method of prompting that aims to find the best prompt to elicit the desired response from a LLM. We do so by maximising a metric called Mutual Information - which indicates the reduction in a model's uncertainty as a result of the prompt.

Entropy

When a language model recieves a prompt as input, it outputs a series of token probabilities sequentially until it reaches the <EOS> token. In the paper, they take the final probability distribution as \(P(Y|X)\) where \(Y\) is the final prediction of the model and \(X\) the prompt.

When we have a probability distribution, we can calculate a probability known as entropy. The lower this value is, the better. This is because a lower entropy value means that the model is more confident in its prediction.

We can calculate entropy with the following formula where \(P(T_i)\) represents the probability of the \(i\)-th token in the final output distribution.

\[ H(P(Y|X)) = \sum_{i=0}^n P(T_i) log (P(T_i)) \]

Mutual Information

We can apply this to the calculation of Mutual Information as seen above.

We'll indicate the calculate of entropy of a probability distribution as \(H(X)\) where \(X\) here represents a final probability distribution. We also assume you have a train dataset of \(n\) examples to use.

  1. First, we choose a set of tokens that are likely to be part of the final answer. This could be words that appear inside the choices we have provided.

  2. Once we've chosen these tokens, we extract out the log probs for each token from our final distribution. We then normalise it so that these new log probs now sum up to 1.

  3. We do this for the \(n\) example inside our train set, this gives us a new distribution \(P(Y_i|X_i)\) for each \(i\)-th example.

  4. We then take the average of these \(n\) distributions to get \(H_{marginal}\)

  5. We then calculate the average of the entropy of each distribution to get \(H_{conditional}\)

  6. We then derive the Mutual Information by taking \(H_{marginal} - H_{conditional}\), the higher this metric the better.

Unsure how to calculate \(H_{marginal}\) and \(H\_{conditional}\)
\[ H_{marginal} = H(\frac{1}{n} \sum_{i=0}^n P(Y_i | X_i) ) \]
\[ H_{conditional} = \frac{1}{n} \sum_{i=0}^n H(P(Y_i|X_i)) \]

We can then use this new mutual information metric to compare the effectiveness of different prompts at eliciting a desired response from our train dataset.

Implementation

Since we don't have access to the raw log probabilites of specific tokens we want in the OpenAI API, we'll instead get the language model to generate a final score from 1 - 10 of its confidence in it's prediction.

We'll then convert this to a probability distribution with two outcomes and calculate a value for the entropy off of that.

Next we'll compare the Mutual Information value for different prompts before choosing what the best prompt is. For this example, we'll be using values from the Story Cloze set.

from openai import AsyncOpenAI
from instructor import from_openai
from pydantic import BaseModel
from typing import Callable, Literal
from textwrap import dedent
import math
import asyncio


class Response(BaseModel):
    chain_of_thought: str
    response: Literal["A", "B"]
    confidence: Literal[
        "Very High Confidence",
        "High Confidence",
        "Moderate Confidence",
        "Low Confidence",
        "Very Low Confidence",
    ]

    def generate_score(self) -> float:
        confidence_scores = {
            "Very High Confidence": 1,
            "High Confidence": 0.8,
            "Moderate Confidence": 0.6,
            "Low Confidence": 0.4,
            "Very Low Confidence": 0.2,
        }
        return confidence_scores[self.confidence]


client = from_openai(AsyncOpenAI())


def prompt_template_1(question: str, options: list[str]):
    assert len(options) == 2
    a, b = options

    return dedent(
        f"""
    You are a world class AI System which excels at understanding complex user stories and generating responses. Output your prediction and also quantify your confidence in your prediction with the following scale.

    - Very High Confidence: The model is highly confident in its prediction, displaying deep understanding, flawless execution, and no noticeable errors.
    - High Confidence: The model is confident in its prediction, with strong relevance and minor errors that do not detract from overall quality.
    - Moderate Confidence: The model has moderate confidence in its prediction, which is generally relevant with some inaccuracies, and meets minimum requirements.
    - Low Confidence: The model has low confidence in its prediction, with limited relevance and several inaccuracies.
    - Very Low Confidence: The model has very low confidence in its prediction, which is largely irrelevant, inaccurate, or incomplete, needing significant improvement


    Context
    {question}

    Options
    A. {a}
    B. {b}
    """
    )


def prompt_template_2(question: str, options: list[str]):
    assert len(options) == 2
    a, b = options

    return dedent(
        f"""
    <prompt>
        <Task>
        You are about to be passed a story. You are to select the correct response from the options provided.

         <confidence-levels>
             <level>
                 <name>Very High Confidence</name>
                 <description>The model is highly confident in its prediction, displaying deep understanding, flawless execution, and no noticeable errors.</description>
             </level>
             <level>
                 <name>High Confidence</name>
                 <description>The model is confident in its prediction, with strong relevance and minor errors that do not detract from overall quality.</description>
             </level>
             <level>
                 <name>Moderate Confidence</name>
                 <description>The model has moderate confidence in its prediction, which is generally relevant with some inaccuracies, and meets minimum requirements.</description>
             </level>
             <level>
                 <name>Low Confidence</name>
                 <description>The model has low confidence in its prediction, with limited relevance and several inaccuracies.</description>
             </level>
             <level>
                 <name>Very Low Confidence</name>
                 <description>The model has very low confidence in its prediction, which is largely irrelevant, inaccurate, or incomplete, needing significant improvement</description>
             </level>
         </confidence-levels>
        </Task>

        <Question>
        {question}
        </Question>

        <Options>
        <option>A: {a}</option>
        <option>B: {b}</option>
        </Options>
    </prompt>
    """
    )


async def generate_response(
    question: str, options: list[str], prompt_template: Callable[[str, list[str]], str]
):
    return await client.chat.completions.create(
        model="gpt-3.5-turbo",
        messages=[
            {
                "role": "system",
                "content": prompt_template(question, options),
            }
        ],
        response_model=Response,
    )


async def generate_responses(
    questions: list[str], prompt_template: Callable[[str, list[str]], str]
):
    return await asyncio.gather(
        *[
            generate_response(
                question=question["question"],
                options=question["options"],
                prompt_template=prompt_template,
            )
            for question in questions
        ]
    )


def calculate_entropy(probs: list[float]) -> float:
    return sum([p * math.log(p) if p != 0 else 0 for p in probs])


def calculate_mutual_information(predictions: list[Response]) -> float:
    probs = [
        [prediction.generate_score(), 1 - prediction.generate_score()]
        for prediction in predictions
    ]

    avg_probs = [0, 0]

    for p1, p2 in probs:
        avg_probs[0] += p1
        avg_probs[1] += p2

    h_marginal = calculate_entropy([i / len(probs) for i in avg_probs])
    h_conditional = sum([calculate_entropy(prob) for prob in probs]) / len(probs)

    return h_marginal - h_conditional


if __name__ == "__main__":
    queries = [
        {
            "question": "Karen was assigned a roommate her first year of college. Her roommate asked her to go to a nearby city for a concert. Karen agreed happily. The show was absolutely exhilarating.",
            "options": [
                "Karen became good friends with her roommate.",
                "Karen hated her roommate.",
            ],
        },
        {
            "question": "Jim got his first credit card in college. He didn’t have a job so he bought everything on his card. After he graduated he amounted a $10,000 debt. Jim realized that he was foolish to spend so much money.    ",
            "options": [
                "Jim decided to devise a plan for repayment.",
                "Jim decided to open another credit card.",
            ],
        },
        {
            "question": "Gina misplaced her phone at her grandparents. It wasn’t anywhere in the living room. She realized she was in the car before. She grabbed her dad’s keys and ran outside.",
            "options": [
                "She found her phone in the car.",
                "She didn’t want her phone anymore.",
            ],
        },
    ]

    best_mi_score = float("-inf")
    best_template = None

    for prompt_template in [prompt_template_1, prompt_template_2]:
        responses = asyncio.run(generate_responses(queries, prompt_template))
        mi_score = calculate_mutual_information(responses)
        print(f"{prompt_template.__name__}: {mi_score}")
        #> prompt_template_1: -0.0781292189485728
        #> prompt_template_2: -0.05907285153542691
        if mi_score > best_mi_score:
            best_mi_score = mi_score
            best_template = prompt_template.__name__

    print(best_template, best_mi_score)
    #> prompt_template_2 -0.05907285153542691